Array 和 LinkedList 的深刻认知
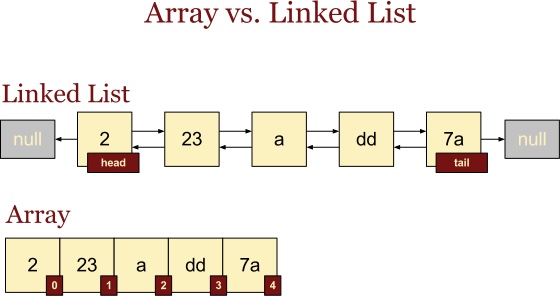
谈数据结构的时候,到底在谈论什么?本质上就是谈论两个东西,分别是 ** 数组 (Array) 和链表 (Linked List)**。
数据物理结构和数据逻辑结构
数组和链表,是数据存储计算机的物理结构,所以叫做数据物理结构。而队列、散列表、堆、树、图等,已经超出了物理结构,是方便我们使用的应用层结构,根据数据的 1-1、1-n、n-1、n-n 逻辑关系,引申出了数据逻辑结构。分别为线性结构和非线性结构,相见下图:
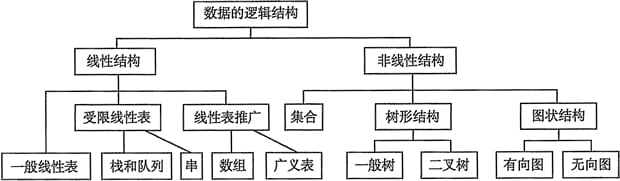
因为我们要使用数据了,所以数据的逻辑形态非常多,这就像应用层协议一样,为了方便我们使用互联网进行数据传输,会有非常多的协议准则。但是数据传输最终只能形成二进制携带 ip 和 port 通过信号传输,所以我们最终处理数据逻辑结构的物理结构只有两个,那就是数组和链表,而很多逻辑结构如完全二叉树、队列等,也都可以同时用数组和链表同时表示。
花开两朵,各表一枝
数组和链表的千差万别又独宠万千的根本原因是什么呢?
其实说到头就和 TCP 和 UDP 的关系一样,他们有各自的优缺点。TCP 和 UDP 磨磨杀杀几十年,谁也没有打败谁,反而都成了互联网传输层协议的中梁砥柱。
数组和链表的关系,也的确成为了花开两朵,各表一枝的比翼鸟。
时间复杂度
数组和链表,如果从直观上来说明不同,那从时间复杂度上来说明再形象不过了。对于数据的增删改查(CRUD),数组和链表的表现是不同的。
因为数据进行增删之前,都需要查找,所以查和增删一定要分开讨论,避免查的时间复杂度影响到增删。
而查到数据后的修改操作,本身不牵涉到时间复杂度,所以改我们可以不用考虑。
我们先看增删两种情况下数组和链表的区别:
数组 -> 增 -> O (n):每次增加一个元素到某个位置,都需要调整其他元素在数组中的位置,进行整体向后 偏移。
数组 -> 删 -> O (n):每次删除某个位置的一个元素,都需要调整其他元素在数组中的位置,进行整体向前 偏移。
** 链表 -> 增 -> O (1)**:加入一个节点,直接更新前后连续 3 个节点的前后驱指针就好。
** 链表 -> 删 -> O (1)**:删除一个节点,直接更新前后连续 3 个节点的前后驱指针就好。
从数据的增删来看,链表是可以秒杀数组的。即使数组对于删的操作进行优化,如假删除,可整体依旧没有链表快。
我们再看查情况下数组和链表的表现:
先说链表,因为链表所有节点的内存地址是不固定的,所以都需要进行一次查找操作。链表的查找只能通过一个节点的前后驱指针遍历查找,所以时间复杂度为 O (n)。
数组数据我们在不生成新数据逻辑结构的前提下,也只能逐个匹配查询,时间复杂度也是 O (n)。
- 如果数据本身是有序的,直接二分查找,时间复杂度为 O (logn)
- 因为我们要获取数据在数组里面的位置以进行增删操作,如果换成二叉搜索树等结构,查询到了数据也没有意义,因为拿不到相对于原数组的位置偏移。
从这里看,查方面,链表和数组打成平手。总体来看,数组是已经输给链表了,毕竟链表的增删复杂度只有 1。
But,这里有个但是,因为数组内存地址连续,所以天然支持随机访问,也就是 array[1] 这样的操作。
我们只要给予数组第一个数据内存地址的相对偏移,就可以根据这个偏移,通过随机访问获取到数据。相比来说,链表的则是顺序访问。
这个大杀器,使得数组的查时间复杂度变成 O (1)。
从这里看,从时间复杂度上面分析,数组和链接各有优势。
内存结构
从上面分析,数组本身已经败落,最后力挽狂澜的优势就是内存地址连续带来的随机访问。
这里就要先说一下数组和链表在内存存储上的差异。这是他们诸多不同的导火索。
数组的内存大小是连续且固定的。不管高级语言怎么做动态数组的优化,这个计算机硬件层面的约束总是跨不过去的。所有数组,都是固定大小的。
也就是我们在申明一个数组空间的时候,内部的元素个数和每个元素的 Size,都已经确定了,那么总大小也是确定的了。
而且,这个空间是连续的空间,即内存地址开始到结束这段区间,都属于该数组,也只能该数组使用。这段区间,可能有 10KB,也可能 100M,根据使用者申请的大小而定。
链表则有很大不同。使用者需要用到节点 (元素) 的时候,才会向系统申请内存空间。而系统分配空间的时候,也仅仅分配申请大小的空间,但这个空间在什么位置,系统不管。
所以使用者需要自己记录每个空间的地址,通过这个地址进行数据的存储。
所以链表的节点空间完全是混乱的,就像一团麻花一样,这一点和数组非常不同。
数组因为空间连续,所以知道开始地址,就能根据元素相对偏移定位到其他地址。而链表的节点空间完全混乱,怎么把节点联系起来呢?
所以链表就走了一个骚操作,每个节点都存储下一个节点的内存地址。这样所有节点形成链结构,就把所有数据串起来了。
所以数组和链表的内存结构十分不同,这样各自有什么好处吗?
内存空间分配
数组因为是连续空间,那么如果没有申请者需要的那么大的连续空间,就分配不了数组空间了。
如果申请者需要申请 10000 个 100KB 元素大小的空间,则需要近 1G 的连续内存空间。如果系统本身还有 2G 内存可供使用,但偏偏没有 1G 连续的空间,那系统因为没法处理,最后只能返回空地址。
链表就不需要连续了,申请者告诉系统需要 10000 个 100KB 的凌乱空间,系统就东凑西凑的一个一个返回给申请者。申请者自己把每个空间地址绑定到需要的节点上,就能使用了。
从这里看,链表比数组的灵活性更大。
细心的你一定发现了,系统返回的空间地址,总归需要存储起来,那每个节点都需要额外 4 个字节用来存储下游节点的内存地址。
那么对于刚才 10000 个元素来说,需要额外的近 40KB 的内存空间才行。所以每个节点,都需要多申请 4 字节的内存。如果对于复杂点的双向链表,就需要多 8 个字节了。
这里也发现,虽然链表与数组相比,虽然申请内存上灵活很多,但是也更费内存一些。
内存空间数量
因为数组的内存空间是固定的,那么在数据操作数组开始申请的大小后,就需要扩容。这个扩容代价还是非常大的。
首先,数组需要申请一块更大的内存空间,然后把之前的内存数据迁移过来,然后才能销毁之前的内存空间。
举上面的例子,如果 10000 个 100KB 的内存空间存满了,当第 10001 个元素进来的时候,就需要再申请 1.5G 的连续内存空间,然后把之前 1G 的数据全部拷贝过来。
所以数组对于扩容有天然的局限性,要处理的事情很多。
链表因为内存空间不连续,就天然免疫了。多一个节点,就向系统再申请 100KB 内存空间,然后串连到链表里面就好。
这里可以看出,链表相比数组,有节点数量上的优势。
内存碎片化
说起内存碎片化,数组和链表都有责任。因为他们都会导致内存碎片。
比如刚才 1G 内存的数组,当数组被清理后,就出现了一个 1G 内存的空洞,这个空洞需要留给其他人用。
如果是 100M,那就是 100M 的空洞,如果是 1M,那就是 1M 的空洞。
空洞大一些,我们感觉不到,因为可分配的余地很大。但是很多这样 1M 或者 10M 的内存空洞,一来不方便利用,二来内存空间里遍地都是,就形成内存碎片了。
那链表呢?也是一样的。因为链表需要频繁的申请内存空间,虽然不知道系统从哪里找来的空间,但链表被销毁后,这些内存空间依旧形成了大大小小的碎片。
所以对于内存碎片,数组和链表都会生成。但有一点,链表处理内存碎片的能力也很强。
链表需要空间的时候,都是一个节点一个节点去讨要的。虽然不知道系统怎么找来的空间,但系统肯定捡碎片来用比较方便,这样可以有效的使用内存空间。
数组因为批量一次性申请,系统很多时候也试着去找碎片空间,但是碎片很多都不符合数组要求。
所以链表相比数组更懂得报恩吧。
数据搬家
数组里的元素想要移动位置就比较麻烦了。因为内存总共就那么大,所有元素都是紧挨着排列的。
那么删除一个元素,就需要把其他元素补上来,增加一个元素,就需要把其他元素踢下去。所以每次元素新增和删除的时候,都挺费事的。这也是为什么数组插入和删除的时间复杂度都为 O (n) 的原因。
删除元素,我们可以通过假删除来优化。即不是物理删除,而是标记删除,这样查找数据的时候发现这个数据已经标记删除,不出处理就好。
那新增元素可就没有这么爽了。一来没有假增加一说,而来如果遇到扩容问题,复杂度又增加许多。
链表还是那么一句老话走天下,因为空间地址不连续,删除新增一个节点的时候,就把上下驱地址变更就好,方便的很。
所以,链表中的节点,还是比数组里的元素待遇好很多,不像数组那么折腾,动不动就要和邻居一起搬家,甚至迁徙风险还很高 (扩容)
随机访问和局部性原理带来的速度!
从上面看,链表相比数组,还是有不少优势的,甚至感觉数组有些多余。
可数组就有一个特性,是链表怎么也无法匹敌的,那就是速度!
对于 CPU 来说,只要给它地址,它就能帮你搞到数据。
因为数组的连续内存空间,所以只要给予相对地址的偏移,就能根据相对地址和偏移,找到偏移数据,这是随机访问带来的好处。
但是链表就没有那么好运了,节点空间都是系统随便给的,根本没有逻辑性,所以访问数据只能一个一个遍历找到对应节点的地址,这也就是顺序访问。
本来随机访问已经比顺序访问带来了很大的速度优势,数组还利用了计算机的高速缓存这趟快车进一步提升了自己的速度,数组真是鬼才。
比较数据获取速度,我们都知道固态硬盘(SSD)大于机械硬盘(HDD),内存条(Memory)大于固态硬盘,三级缓存(L3 Cache)大于内存条。现代计算机都有一级缓存(L1)、二级缓存(L2)、三级缓存(L3),其实一级缓存的速度已经非常非常快了,随机访问延时能达到 1ns,相比来说,内存延时有 100ns。
数组和链表数据都是在内存里的,如果访问数据的时候,能够顺带多访问一点数据并放置到 L1 L2 L3 缓存中,后期直接访问多级缓存,而不再去内存拿数据,那对于 CPU 来说可就太棒了,终于不用去等慢的要死的内存条了。
前辈们探索发现了存储器中的数据局部性原理。
当一个数据被访问,那么它短时间内很可能再次被访问,这是时间局部性。
当一个数据被访问,那么它相邻的数据很可能很快被访问,这是空间局部性。
当然,局部性原理里面说到的数据,不仅仅是数组里面的数据,还包括指令。但这已经完全够数组消化的了。
数组中某个元素被访问后,CPU 会顺带预读相邻的一些数据,一起从内存中读走并放置到高速缓存 (一级、二级、三级) 中。后面读取其他元素的时候,直接从高速缓存中读取了,都不过内存了。
数组利用了空间局部性提升自己的速度,比如遍历 100W 和 150W 数组数据的时候,一个耗时 100ms,一个耗时 110-120ms,耗时并不根据数组数量线性变化,就是这个原理。
链表没有搭上随机访问这趟列车,也搭不上高速缓存这趟快车,速度上已经落后数组不是一点点了。
总结
链表很多方面的确优与数组,但速度上就落后数组很多了。在速度和时间就是一切的大前提下,数组成功扳回了举足轻重的一局。
其实数组和链表还有很多细节可以讨论,比如数组在数学运算上更胜一筹,尤其二维数组做矩阵运算效率极高。而散列表和链表一起使用,就是规避数组和链表的各自不足。
数据逻辑结构,最后底层都会通过数组或链表实现,有些只能通过数组或者链表单一实现,有些则两者均可。还会根据机器配置等客观因素进行考量。
数组和链表各自开了两朵美丽的花,一起为算法撑起来物理基础。
算法串联数据,如脊贯肉;
数据实化算法,如肉附脊。
— 郑晖《冒号课堂》